导读关联搜索是指在知识图谱(KG)中搜索与查询实体关联的排到前面的实体。关联性往往是模棱两可的，尤其是对于像DBpedia这样的模式丰富的知识图谱，因为它支持基于多种关系和属性的不同语义的关联性。由于用户可能缺乏将所需语义正规化的专业知识，由此出现了监督的方法，以便从用户提供的示例中学习隐藏的用户定义的关联性。基于此，本文提出了一种基于KGs的关联搜索生成模型-GREASE。该模型适用于基于元路径的关联，其中元路径描述了待查询实体与答案实体关联的特定的语义类型。它还扩展了支持约束答案实体的属性。在两个大型KG上进行的大量实验表明，GREASE在有效性，表达力和效率方面已达到了最新水平。

介绍
背景：在知识图谱(KG)中，节点是与属性关联的实体，并以二元关系作为边进行互连。越来越多的KGs出现在不同的领域，其中一些可以像Linked Open Data使用。主要领域的KGs通常有一个简单的模式，例如，LinkedIn KG 描述专业领域的成员、公司和其他实体。还有一些通用的KGs提供百科知识，因此有一个丰富的模式，其中包含数千种关系和属性的类型，比如DBpedia。我们以图1中的KG为本文的介绍示例。它描述了电影、演员、导演和奖项。

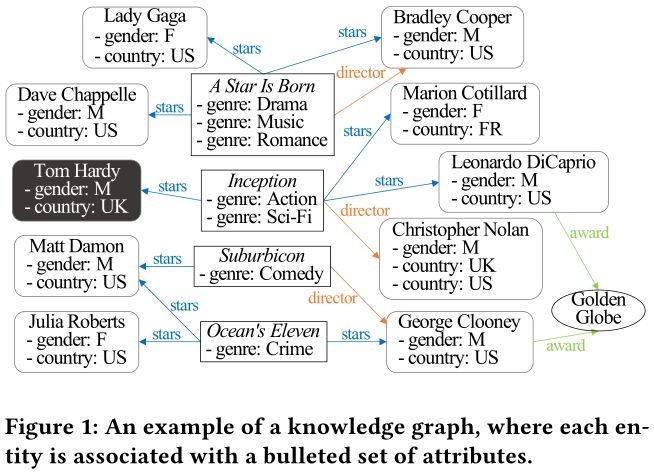
目前，基于KG的关联搜索本质上是搜索KG中与输入查询实体最关联的实体。然而，关联性具有广泛的含义，特别是对于一个模式丰富的KG。例如，给定Tom Hardy作为查询实体，用户可能会搜索到与他合作的女演员，或与他合作的美国导演。不幸的是，非专业用户缺乏正式描述所需的关联性语义的专业知识，因为正式化查询语言和丰富的KG模式都很难学习。
问题：为了弥补非专家用户和结构化KGs之间的差距，一个切实可行的解决方案是要求用户提供少量的例子，然后通过这些例子去学习用户定义的关联性。用户可以以有序的查询实体-答案实体对的形式指定一个示例，用来说明所需语义的关联性。例如，两个不同的用户可以提供不同的例子集合:
用户提供的S1旨在去发现和Tom Hardy关联的实体就像Lady Gaga与 Dave Chappelle的关系，以及Julia Roberts与Matt Damon的关系一样。潜在的语义可能就是演员，最好是与汤姆·哈迪合作的美国女演员。在这种情况下，Marion Cotillard和Leonardo DiCaprio是可以接受的答案。用户提供S2有不同的需要，主要是寻找与Tom Hardy合作的美国男导演或演员。那Leonardo DiCaprio和Christopher Nolan成为了最佳答案。
挑战：它通常假设用户定义的关联性可以由一个或多个元路径表示。元路径是一个关系类型的序列，即模式级别的路径。例如，S1下的共同主演的关系具有以下元路径特征：
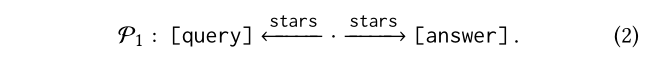
S2下的合作关系部分由P1表征，部分由：
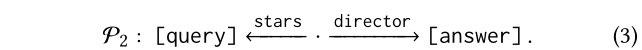
这些方法的关键挑战是元路径的选择和加权。现有的方法训练判别式模型直接从用户提供的样本中学习元路径的权值，但存在以下局限性。
他们的判别式模型依赖于负样本，并且当用户只提供正样本时采取自动采样方式。但是，识别高质量的负样本是对算法和计算能力的要求很高。
它们主要关注基于元路径的关联性，但是不支持上面示例中的属性的表示，比如性别和国籍。它们描述用户需求的能力有限。
贡献：在这项工作中，我们解决了这两个挑战并提出了GREASE，一个新的基于KG的关联搜索生成式模型 。我们并开源了实现的代码。我们的贡献总结如下：
我们将元路径的权值视为后验概率，并设计一个具有成本效益近似值的生成模型。我们的模型不依赖于反例，并且在实验的有效性和效率上都优于现有的方法。
我们扩展了模型，不仅支持基于元路径的答案实体与查询实体的关联性，还支持约束答案实体的属性。扩展允许表示更具有表达性的用户定义的关联性。
问题定义
设R表示所有实数的集合。我们假定实体V、关系类型R、属性类型A和属性值L是可数的不相交的集合。
定义（知识图谱）一个知识图谱（KG）是一个 有向图表示为G=<V,E,Ψ>,其中V ?V是一个实体表示的有限的节点集。E ? V × R ×V是表示为有向边的实体之间的有限关系集。且Ψ : V → P(A × L)其中P(·)表示幂集（是指一个集合的所有子集），是一个将每个实体v ∈ V与有限的属性集关联起来 Ψ(v) ? A × L的函数。
对于实体v ∈ V，它的属性包括：
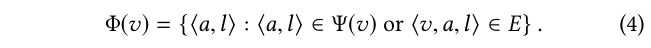
比如，在图1，Suburbicon的属性包括一个属性 ?genre, Comedy?和2个关系 ?stars, Matt Dameon?和 ?director, George Clooney?。
我们用标准的方式定义路径。它是非循环的，它的边不需要遵循相同的方向。然而，在论文的其余部分，我们总是写出右箭头并重写左箭头←(r)为→（r_-1），其中r_-1表示 r ∈ R 的逆向。我们把一条路径p：v0→v1→...→vl从v0到vl简写为v0 ~p vl。路径的长度就是其边的数目。
定义（元路径）元路径是关系类型P的序列：r1 r2 ... rl，其中 r 1 ,.. .,r l ∈ R是关系类型（或它们的逆）且l是P的长度表示为 len(P) = l 。如果p是以p的形式：v0→v1→...→vl，则一条在KG沿着P的路径p表示为 p |= P 。
例如，在等式中所示的两个元路径(2)和(3)正式定义如下：
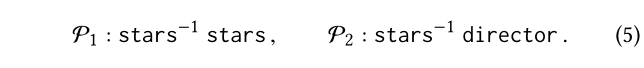
它们的长度均为2。P2的路径如下：
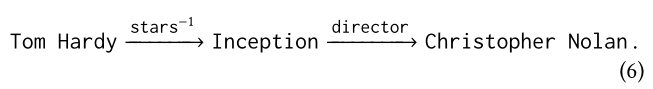
定义(关联性搜索) 给定用G=<V,E,Ψ>表示的KG，设rel：V×V→R是用户定义的真值函数。对于u，v∈V，rel(u，v)返回的是v对u的关联性。设 k < |V|是一个预设定的正数。对于一个查寻实体q ∈ V，关联性搜索就是查找top-k的答案实体Ans(q) ? (V \ {q})，其对rel而言是与q最关联的。
按照[9，15，22]，我们假设用户提供少量有序的查询-答案实体对作为示例，以举例说明搜索系统无法直接访问的所需的rel。 
定义(按实例进行的关联性搜索)。该问题扩展了关联性搜索定义，在由S表示的一组用户提供的示例的监督下，转化为学习函数rel。每个示例都是有序的查询答案实体对?s，t?∈V×V，其中s称为源实体，t是目标实体，因此v∈ans(q)与q关联，就像t与s关联一样。
例如，(1)中的S1和S2是查询实体Tom Hardy的两组示例。它们表示不同的rel函数。
生成式关联模型
根据按实例进行的关联性搜索定义，rel函数是以一组用户提供的示例S为条件的，因此我们将rel(q，v)重写为rel(q，v/S)。以前的研究计算都是基于元路径的关联性。同样的，我们将rel分解成一组元路径上加权关联的线性组合表示为Ω mp = {P1 ,.. .,P n }：
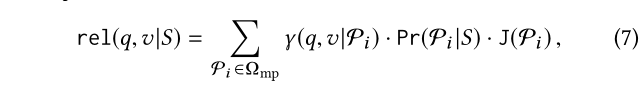
其中  γ(q,v|P i )度量v到q关于指定的元路径Pi的实值关联性，Pr(P i |S) 表示Pi的权重以及J(Pi)是一个避免过拟合的正则化项。元路径及其权重都是要从S中学习的。例如，在(1)中的S1，在(5)中的元路径P1应该拥有较大的权重，因为对于每个S1中的例子，图1中都存在一条路径都够沿着P1连接源实体到目标实体。
为了建立rel函数，我们描述了 Ω_mp的选择以及γ、Pr和J的计算。
元路径选择
以S为例，我们选择了基于S的Ω_mp。我们的Ω_mp包含所有来自从S的可能的元路径。如果KG中存在路径，且使其沿着Pi，并在某个用户提供的示例中将源实体连接到目标实体，则元路径Pi位于Ω_mp中：

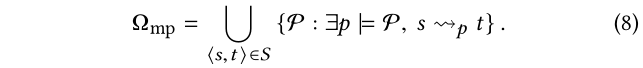
 基于关联性的元路径
关联对于度量v与关于指定的元路径Pi的q的关联性，目前已经进行了大量的研究。这超出了本文的重点，我们将路的径数目扩展为我们的度量因素：
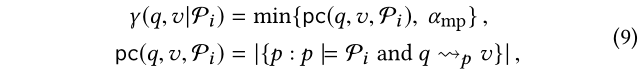
其中，pc(q,v,P i )表示在KG中沿着Pi能够连接q和v路径的数目，且α_mp>0是一个参数，主要是用来限制pc的大小以及防止有较高的倾斜值。比如在图1中，对于(5)中的P2，可得到：
因为在(6)中只存在一条路径其沿着P2且能够连接 Tom Hardy 和 Christopher Nolan。
生成式元路径权重
加权策略是rel函数有效性的关键，也是我们工作的重点。与现有的判别式方法不同，我们将权重Pr(Pi/S)作为后验概率，并提出了一个新的生成式模型。在下面，我们还将使用Pr(·)来表示事件的概率。我们根据KG估计概率，并从S中学习Pr(Pi/S)。具体的，我们使用贝叶斯定理重写Pr(Pi/S)：
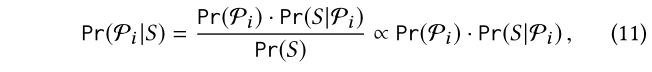
其中后验概率Pr(Pi/S)是和先验概率Pr(Pi/S)乘以似然Pr(S/Pi)成正比的。下面我们分开计算先验概率和似然。
先验概率的计算：对于先验概率Pr(Pi/S)，需要考虑到元路径是关系类型Pi：r1 r2 ... rl的序列。我们假设，在前面(i?1)关系类型r1 r2 ... ri-1的上下文历史中观察到第i个关系类型ri的概率可以用在前面关系类型ri-1的短上下文历史中观察到它的概率来近似，即一阶马尔可夫性质。这一假设是合理的并且在图上也是很常见的。特别地，图上的随机游走也满足这个性质。我们得到：
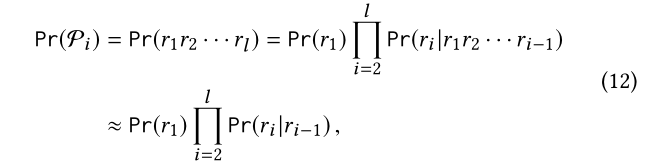
如果我们从频率计数中估计Pr(r1)和Pr(ri|ri?1)，则这反过来将产生以下估计的Pr(Pi)：
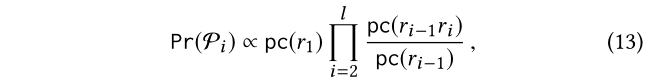
其中pc(P)表示KG中符合元路径p的路径数：
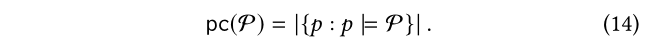
在(13)中，可以根据(14)计算pc，由于这些元路径是非常短的，大小不会超过2，所以计算是很快的。比如，在图1中，对于在(5)中的P1和P2，我们得到：
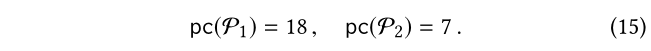
与此同时，由于Pi的相反方向也是有意义的，我们可以利用在随后的关系类型ri+1的上下文历史中观察到第i关系类型ri的概率，然后以类似的方式进行假设和估计概率：
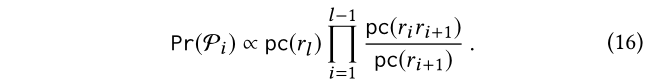
为了提高模型的鲁棒性，我们采用了(13)和(16)的算术均值作为Pr(Pi)的终值。
对于一个长的元路径P。这一近似是有用的，因为在很大的KG上,当p长时，它计算准确的频率计数的函数可能是不可行的。对于P：r1r2···rl，设apc(P)表示pc(P)的这种近似。我们得到：
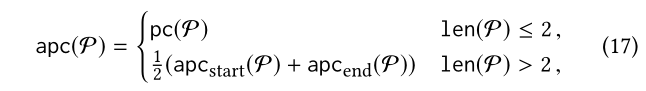
其中，apc-start和apc-end分别表示(13)和(16)的右侧，这个近似在后边会用到。
似然的计算：对于似然Pr(S|Pi)，一般认为S中用户提供的例子是条件独立的Pi:
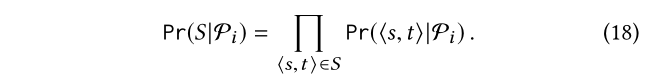
Pr(?s，t?|pi)表示沿着Pi的路径连接s到t的概率，我们从频率计数中估计这个概率：
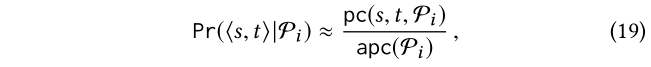
其中， pc(s,t,Pi)是由(9)计算得到的，且apc(Pi)是由(17)计算得到的一个近似值。
为了提高模型的鲁棒性，需要进行平滑处理，以避免pc(s，t，Pi)=0的情况，但是反过来会导致Pr(S|Pi)=0。所以在这种情况下，我们把pc(s，t，Pi)的的0值用下面的较小非0值来代替：
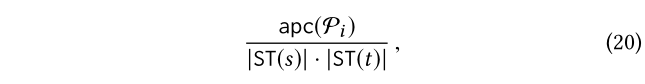
其中 apc(P i )是由(17)计算得到的，ST(·)表示与给定实体具有相同(很具体)类型的一组实体。类型是出现在几乎每个KG中的一个属性。上面的值表示Pi之后的平均路径数，并将两个类型相同的实体连接为s和t。
正则化
长的元路径是复杂的，可能会超出用户提供的例子范围.我们对Pi的复杂性加了惩罚项。具体来说，我们用以下正则化惩罚长的元路径：
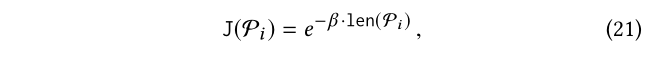
其中len(Pi)表示Pi 的长度，且 β >0是一个衰减系数。
扩展基于面的关联性
以前的研究只计算基于元路径的关联性。我们将元路径扩展到面。面要么是元路径，要么是约束答案实体的属性。相应地，我们通过在一组属性上添加加权关联的线性组合来扩展(7)中的rel函数用Ω_pro={?a1，l1?，...，?a1，l1?}：
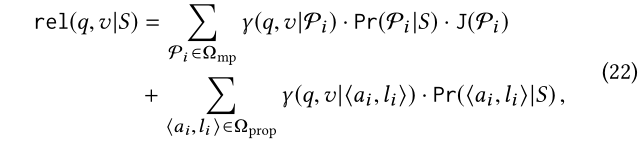
其中，γ(q,v|?a i ,l i ?)是度量v与关于指定的元路径Pi的q的关联性， Pr(?a i ,l i ?|S)表示 ?a i ,l i ? 的权重。属性已经很简单，因此不需要重新划分。属性及其权重也可以从S中学习。例如，在(1)中的S1有两个属性?gender, F?和?country, US?应该具有较大的权重，因为它们约束了S1中的所有目标实体。
为了建立扩展的rel，下面我们描述了 Ω_prop的选择，以及属性的γ和Pr的计算。
属性选择
如果一个属性在某个用户提供的示例中约束了目标实体，则该属性?a i，l i?就在Ω_prop中：

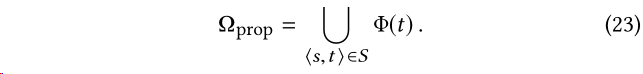
基于属性的关联性
我们测量v关于?a i，l i?的关联性。根据?a i，l i?是否是约束v的属性，它是独立于q的：
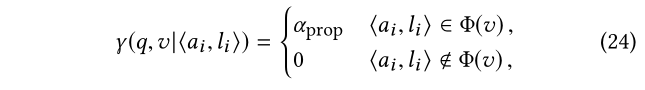
其中，α_prop>0是一个参数，用于在扩展rel计算中调整属性相对于元路径的重要性。
生成式权重
类似于我们的加权元路径的生成式模型，我们将加权P(?a i，l i?x s)看作后验概率，并用贝叶斯定理重写它：
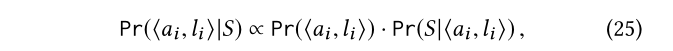
其中，后验概率Pr(?a i ,l i ?|S)是和先验概率Pr(?a i ,l i ?)乘以似然Pr(S|?a i ,l i ?) 成正比的。下面我们分别计算先验概率和似然。
先验概率计算。对于先验Pr(?ai，li?)，它表示了属性?ai，li?约束KG中一个实体的概率，我们根据频率计数中估计这个概率：
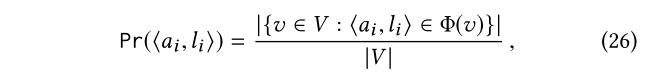
其中V是在KG中实体集合。
似然计算。似然Pr(S|<ai,li>)类似于(18)，对于给定的<ai,li>，用户在S中提供的例子被认为是条件地独立的：
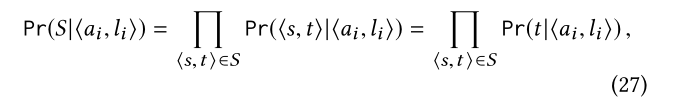
其中最后一个等式之所以成立，是因为属性?ai，li?约束对应于用户提供的示例中的目标实体t的答案实体，因此?ai，li?与示例中源实体s相互独立的。
Pr(t|?ai ,li ?)表示一个实体受到<ai,li>约束是t的概率,它是我们根据频数来估计的：
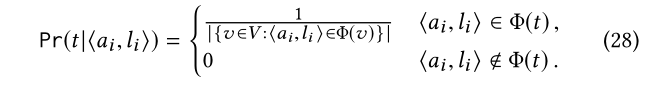
为了提高模型的鲁棒性，需要进行平滑处理，以避免 Pr(t|?a i ,l i ?)=0的情况，但是反过来会导致 Pr(S|?a i ,l i ?)=0。所以在这种情况下，我们把 Pr(t|?a i ,l i ?)的0值用下面的较小非0值1/|V|来代替。
搜索算法
最后，我们给出了一个有效的实现，以支持在线环境中从用户提供的示例中学习所提出的模型并迅速返回答案实体。

算法
完整的GREASE算法如图2所示。MPSearch(line 1)中的Ω_mp是由(8)计算得到的。它对S中的每个示例执行一次双方向搜索，同时从源实体和目标实体开始。搜索空间被限制为不超过L的元路径，这是预先确定的上界。Ω_mp和Ω_prop组成Ω(第3行)，即所有的面(22)中计算rel的方法。对于每个面Ωi∈Ω，我们要根据上述的计算Pr(Ω_i|S)(第4-6行)。m在Ω_mp元路径最大权重的用Ωtop表示(第7行)。在Ω_top候选答案实体中，所有从q通过一条沿着元路径的路径连接的实体用C表示(第8行)。这里，出于效率考虑，我们只使用m元路径来识别候选答案实体。对于每个候选答案实体，计算它与q的扩展关联性(第9-11行)，并返回k个排名最高的实体。
实验结果


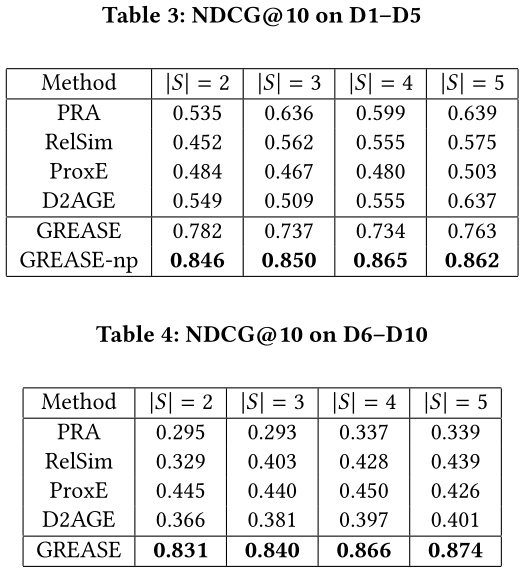
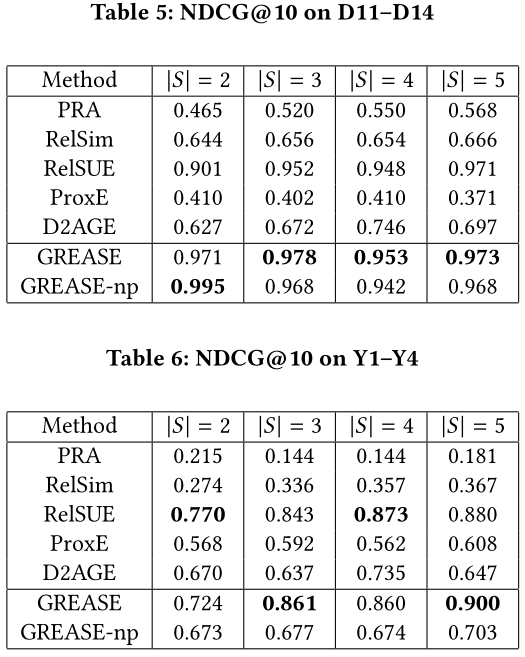
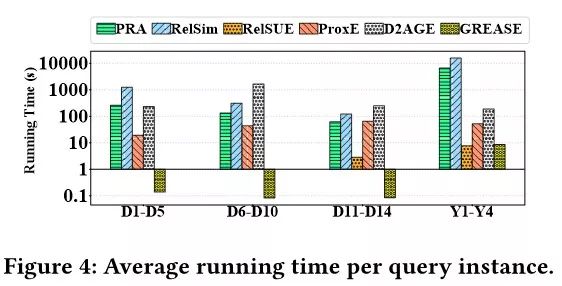
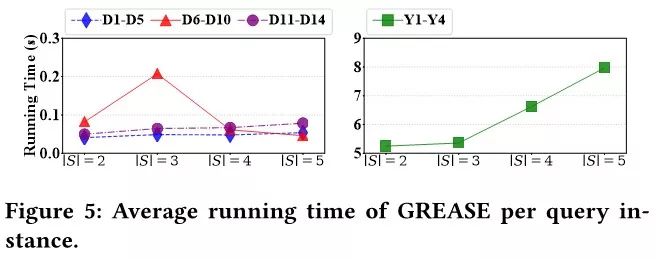
结论
 我们提出了一种新的基于KGs关联搜索方法—GREASE。与现有的方法相比是有区别的，GREASE通过其更有效的元路径加权生成模型，它更具有表达性，基于面的表现与之关联属性及其实现的高效率。这些技术贡献已在大量的实验评估中得到证明。
我们的方法的一个局限性是，我们对概率的估计主要基于KG中的频率计数。然而,现实世界中的KGs可能是不精确的或不完整的，这是可能影响我们估算的准确性。我们使用了平滑方法来部分解决这个问题，但进一步的尝试可能是有帮助的，比如利用外部知识。在今后的工作中，我们将继续努力还可以考虑使用本体论模式和推理服务处理更复杂的关联性语义。
请关注专知公众号（点击上方蓝色专知关注）
后台回复“GREASE” 就可以获取《GREASE：A Generative Model for Relevance Search Over Knowledge Graphs 》的下载链接~
-END-
专 · 知
专知，专业可信的人工智能知识分发，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取更多AI知识资料！欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程视频资料和与专家交流咨询！
请加专知小助手微信（扫一扫如下二维码添加），获取专知VIP会员码，加入专知人工智能主题群，咨询技术商务合作~点击“阅读原文”，了解注册成为专知VIP会员