重要事情说在前面，耀华中学的这道题真的可以入围天津市2019年年度高三数学经典问题前三名了，非常有意思的一道八个零点问题，考查周期性，考查观察题意区间开闭问题，考查画图技能，临界条件的把握，还考查能否观察出简易方法确定临界条件（我发现了
![]()
），这是一道非常值得思考的经典问题。
如何审题？如何切入？
1.两个函数均为周期函数,经分析易知：f(x),T=4; g(x),T=2
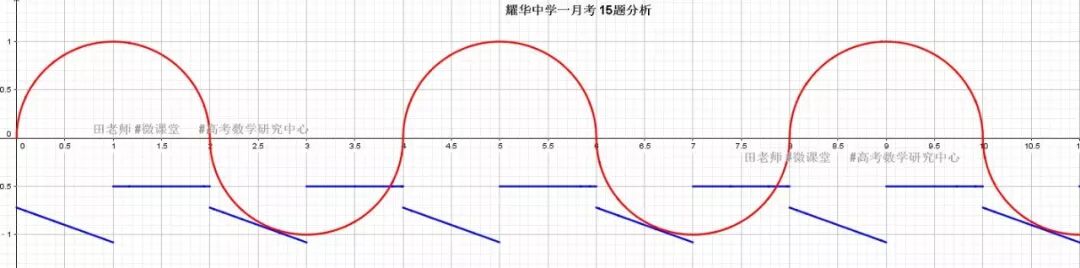
2.f(x)的图像为以(1,0)为圆心，1为半径的上半圆,经过周期循环如图所示。K影响g(x)的斜率,即直线倾斜程度。3.抓住临界条件为解题关键。
使用动图分析此题（这么经典的问题，我一定做个gif给你看看它有多优美）,
如图所示：
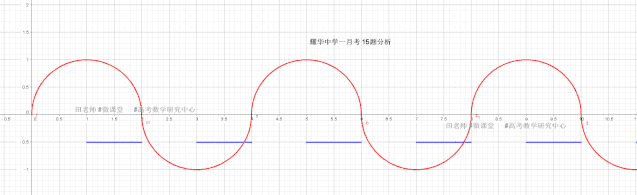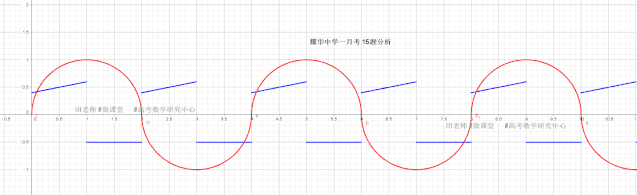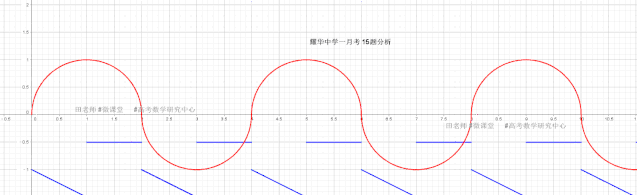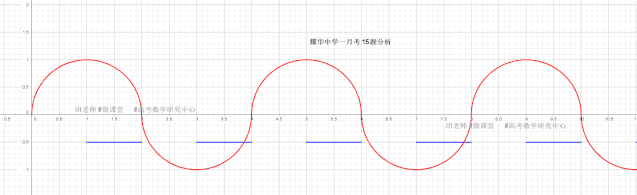
局部放大：
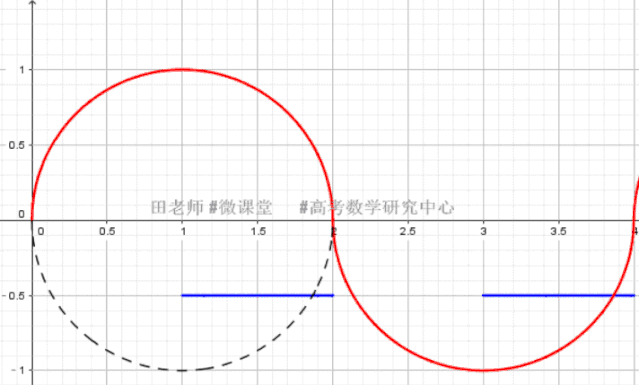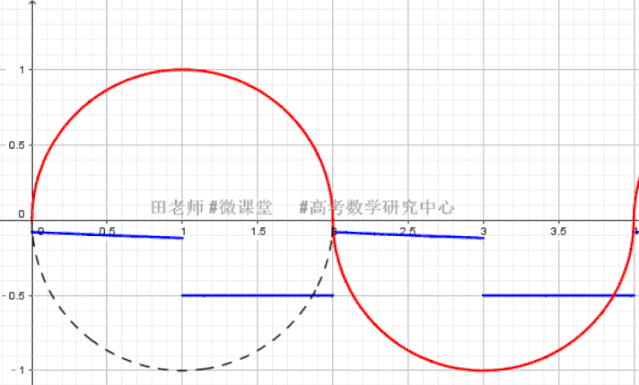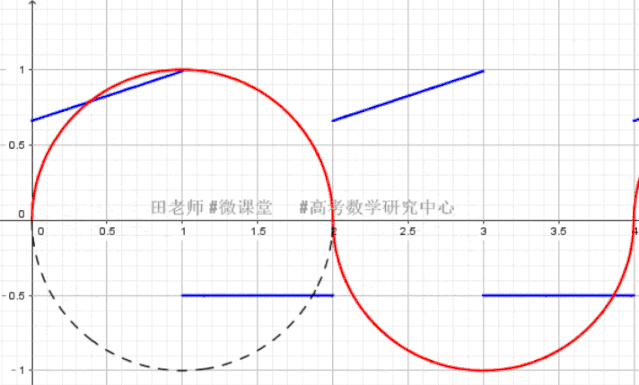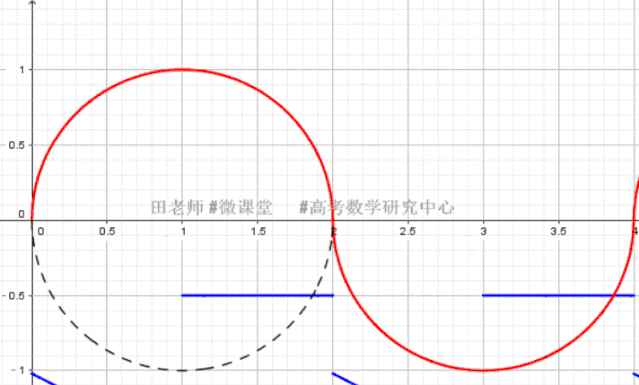
临界条件确定的方法:
(让我们虚拟一个半圆,将问题限制在"第一个周期"内进行分析):
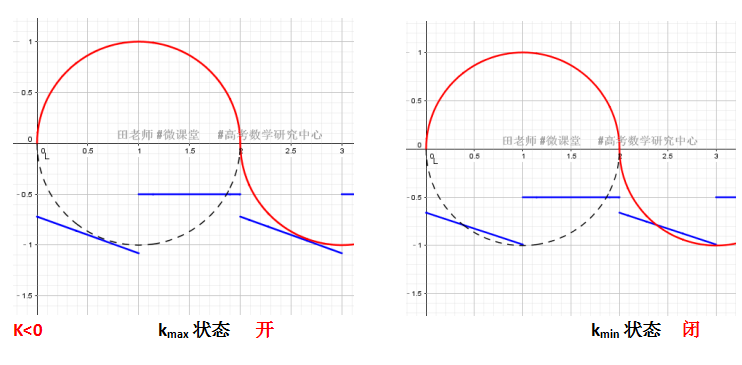
(1) K<0 时,直线与半圆相切,利用圆心到直线的距离=1,可计算此时Kmax,而kmin的确定是直线经过圆上点(1,-1)
解得
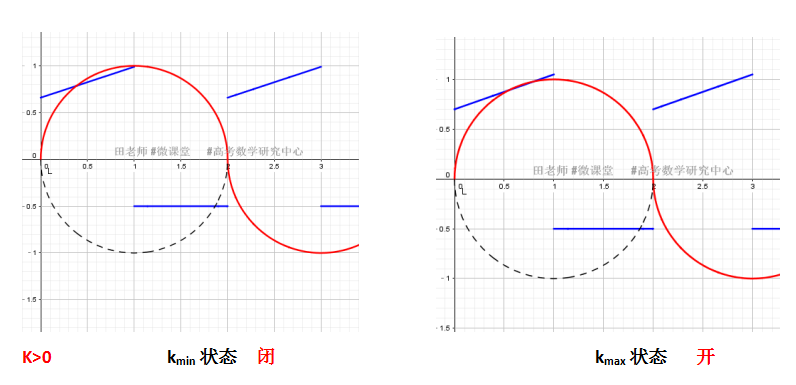
(2) K>0 时,直线与半圆相切,利用圆心到直线的距离=1,可计算此时Kmin,而kmax的确定是直线经过圆上点(1,1)
解得
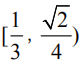
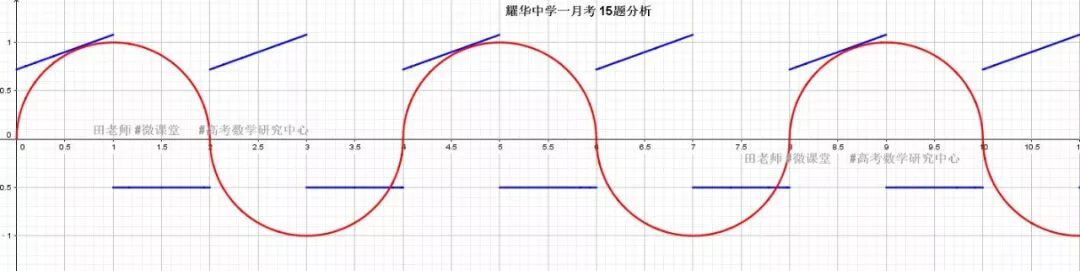
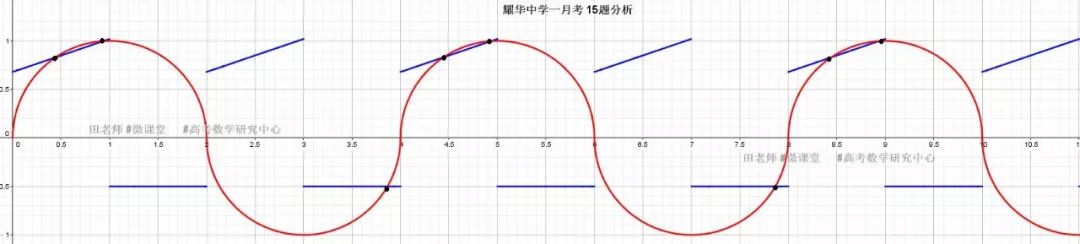
(3) K=0 时,居然符合题意(隐蔽的陷阱，不分析这个状态，一律扣五分
![]()
)
同学们！这道题和2017年南开区一模选择8很像，尽管已知条件里0是开区间，但是人家求[0,11]（这里出题人把它猝不及防地改成了闭区间），所以f(0),g(0)的计算要根据T去计算，而不是利用函数解析式计算。经分析，K=0是符合题意的，如下图所示：
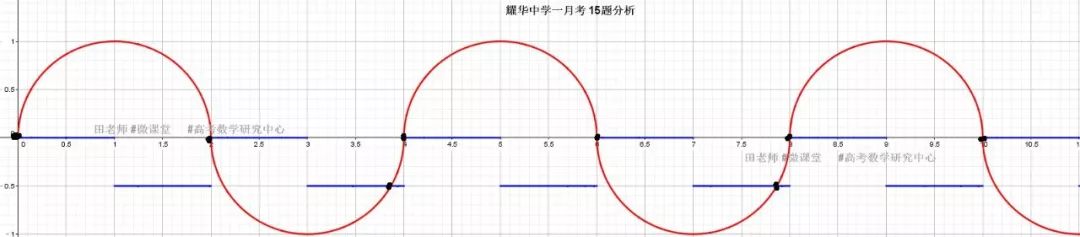
综上：
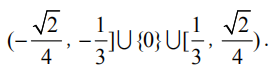
感谢浏览
![]()
如果你有更好的解题思路，记得后台留言和田老师一起讨论:）
欢迎扫码关注
每天解析市五所数学典型题
![]()
），这是一道非常值得思考的经典问题。
)
如果你有更好的解题思路，记得后台留言和田老师一起讨论:）
